Físico de RUDN University desarrolló un programa para determinar la estabilidad de los agujeros negros

Los agujeros negros, cuya existencia predijo la teoría general de la relatividad de Einstein, son objetos con una atracción gravitacional tan fuerte que ni la luz puede abandonarlos. Estos densos y masivos objetos distorsionan el espacio-tiempo, un modelo en el que tres dimensiones espaciales se complementan con una cuarta temporal. Muchos modelos matemáticos que describen agujeros negros incluyen correcciones para ajustar esta curvatura y la condición clave para cualesquier de estos modelos es su estabilidad con pequeños cambios en el espacio-tiempo. Los agujeros negros inestables matemáticamente no tienen ningún sentido físico, es decir, los objetos que describen no pueden existir. Por ello, un físico de RUDN University propuso un método para hallar los parámetros bajo los cuales se producirían agujeros negros inestables en el modelo espacio-tiempo.

«La estabilidad de un agujero negro ante pequeñas perturbaciones del espacio-tiempo es una condición necesaria para la viabilidad del modelo en consideración. Agregar correcciones a la ecuación de Einstein es uno de los enfoques más prometedores para desarrollar teorías alternativas de la gravedad. Un papel importante juega la corrección de cuarto orden de Gauss-Bonnet y su generalización a órdenes superiores (teorema de Lovelock)», explicó Roman Konoplya, investigador del Instituto Científico y Educativo de Gravedad y Cosmología de RUDN University.

El físico de RUDN University estudió la estabilidad en la teoría de Einstein-Gauss-Bonnet, donde la ecuación de Einstein describe un agujero negro con un cuarto término adicional. Previamente, el físico estudió un problema similar para otro modelo matemático de agujeros negros, la teoría de Lovelock. En ella, un agujero negro se describe mediante la suma de un número infinito de términos. Resulta que el área de inestabilidad está firmemente relacionada con los valores de las constantes de acoplamiento, coeficientes numéricos, por los cuales se multiplican las correcciones introducidas en la ecuación de Einstein.

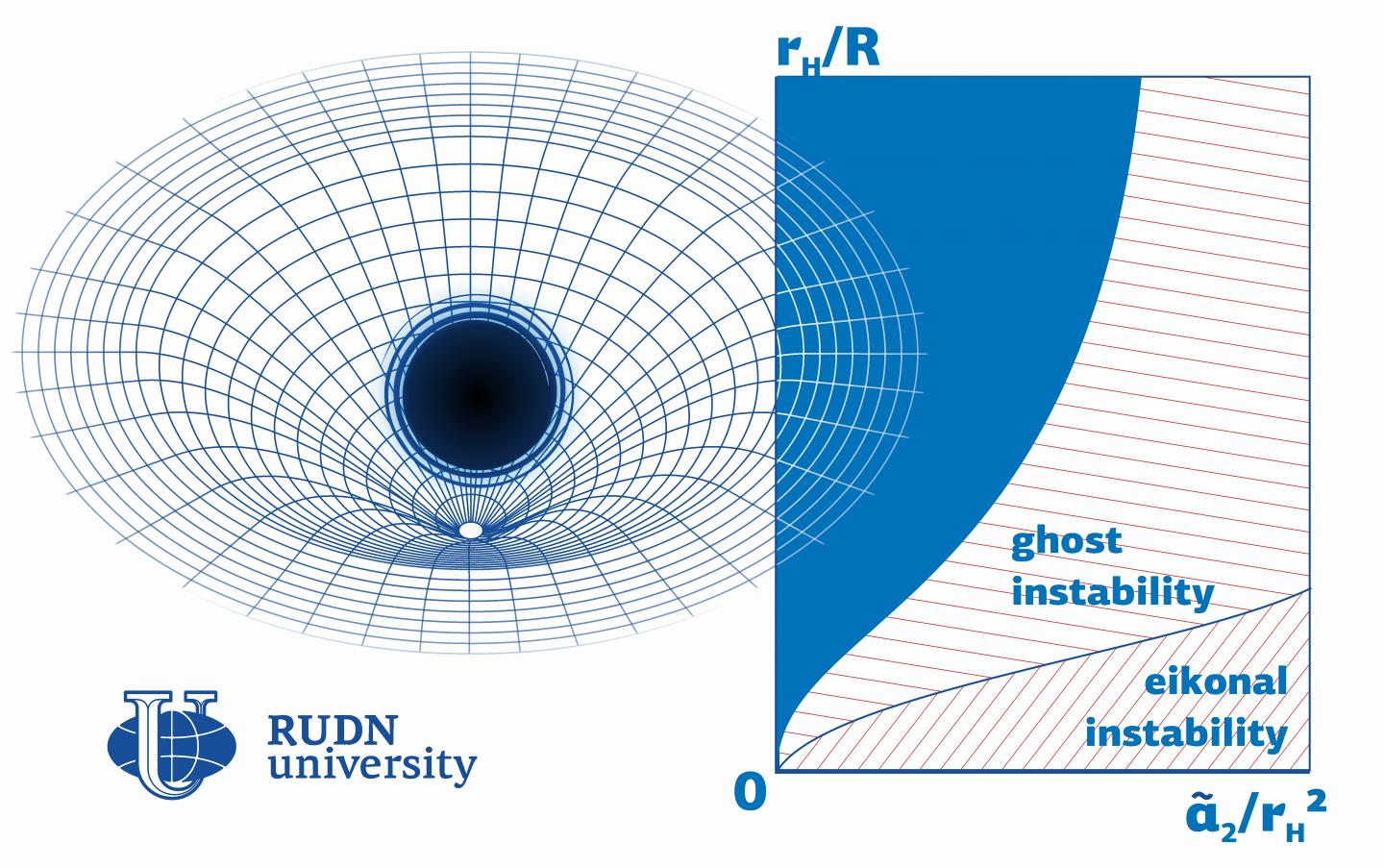
El físico de RUDN University demostró que los agujeros negros pequeños no pueden existir en el modelo de Einstein-Gauss-Bonnet. Si las constantes de acoplamiento son lo suficientemente grandes en comparación con otros parámetros (por ejemplo, el radio del agujero negro), el modelo casi siempre es inestable. Para los valores negativos de la constante de acoplamiento, el área de estabilidad es mucho mayor. Con base en estos cálculos, el físico y su equipo han creado un código fuente que permite introducir cualquier parámetro y calcular si un agujero negro será estable o no.

«Lo que proponemos permite probar la estabilidad de los modelos de agujeros negros. Los colegas pueden usar el código que hemos publicado para construir una región de inestabilidad para modelos con un conjunto arbitrario de parámetros», expresó Roman Konoplya, investigador del Instituto Científico y Educativo de Gravedad y Cosmología de RUDN University.

La investigación fue publicada en Physics of the Dark Universe.