El matemático de la RUDN describió por primera vez el movimiento de las ondas en una cinta de plasma plana

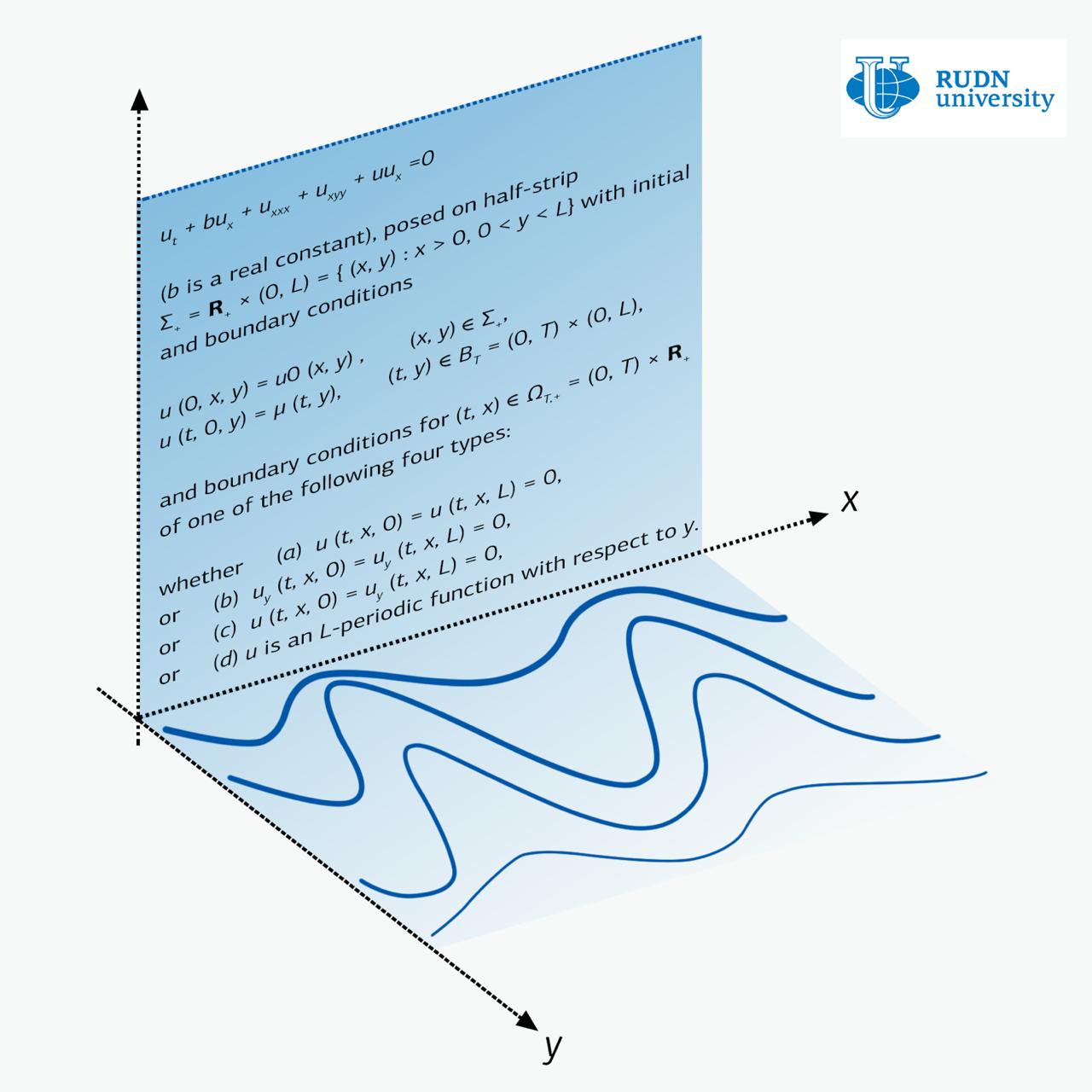
La ecuación de Zakharov-Kuznetsov es una ecuación para una función de dos variables x e y. Desde el punto de vista de la física, x es la dirección de propagación de la onda, y la deformación del medio ocurre a lo largo de la dirección perpendicular y. Entonces, por ejemplo, la oscilación de una cuerda de guitarra se ve como: una onda corre a lo largo de la cuerda, mientras que las oscilaciones ocurren en una dirección perpendicular a la carrera de la onda.

Hay una gran cantidad de resultados que describen soluciones de las ecuaciones de Zakharov-Kuznetsov en el caso donde no hay restricciones para y. Pero el tema de la propagación de ondas en la banda, cuando y está acotado, ha sido poco estudiado hasta hace poco. Y esto a pesar del hecho de que tal declaración del problema tiene un significado físico y, por lo tanto, aplicaciones potenciales.

Los matemáticos de RUDN descubrieron la ecuación de Zakharov-Kuznetsov en la tira. Estudiaron tres casos principales: cuando no hay banda de oscilación en el límite, cuando no hay corriente en el mismo límite y cuando las condiciones del límite tienen una estructura periódica. El último caso corresponde a la propagación de ondas en un medio cuya estructura es periódica en x.

En todos estos casos, los matemáticos pudieron demostrar la existencia y los teoremas de singularidad de las soluciones. Para los sistemas de ecuaciones diferenciales parciales, que incluyen la ecuación de Zakharov-Kuznetsov, tales ecuaciones son muy raras. Para soluciones de la ecuación con condiciones iniciales en la tira, estos son los primeros resultados similares. Los flujos de plasma plano con condiciones límite consideradas por los científicos de la RUDN pueden ocurrir en física y astrofísica.

Las ecuaciones de Zakharov-Kuznetsov pertenecen a una clase más amplia de ecuaciones, conocidas como ecuaciones de Kortweg-de Vries. Al estudiar esta clase de ecuaciones por primera vez, fue posible describir solitones: ondas cuya forma no cambia durante el movimiento. Los físicos ven los solitones como una herramienta para el funcionamiento de los sistemas modernos de transmisión óptica de datos. El estudio de los solitones que pueden surgir en las ecuaciones de Zakharov-Kuznetsov es una de las opciones para el desarrollo del trabajo realizado por matemáticos de la Universidad RUDN.

Artículo en Nonlinear Analysis: Real World Applications