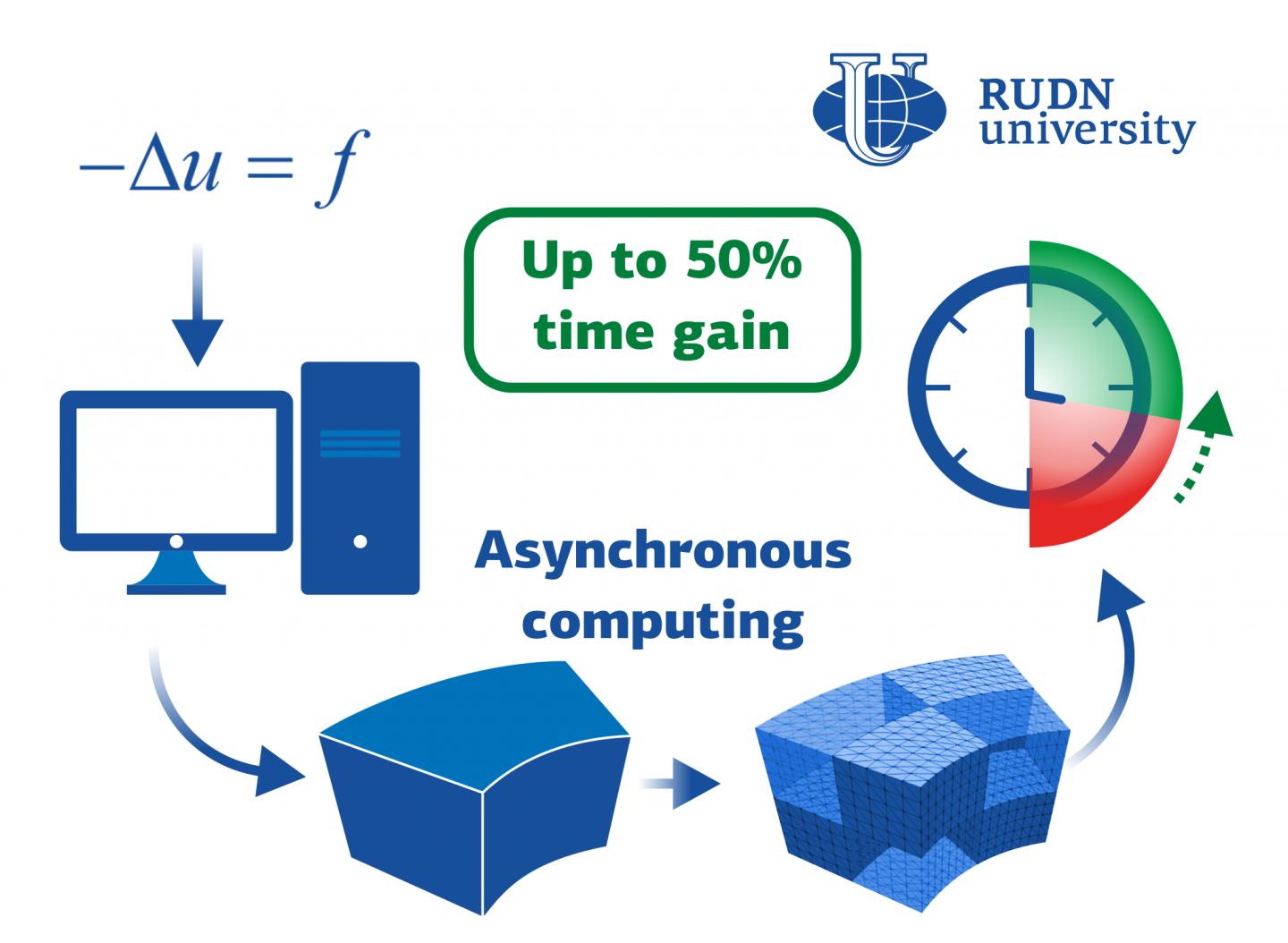
Matemático de RUDN University aceleró el método de descomposición para la computación paralela asincrónica

Los métodos de computación paralela se utilizan a menudo para calcular problemas de física, ingeniería, biología y de otras áreas. El principio de la computación paralela consiste en que varios procesadores unidos a una red resuelven simultáneamente un mismo problema, cada uno soluciona una pequeña parte de este. La forma de dividir el trabajo entre los procesadores y organizar la "comunicación" entre ellos se elige en función de las características del problema a resolver. Uno de los posibles métodos es el de descomposición. El área de estudio se divide en diferentes partes o subdominios, depende del número de procesadores. En tales casos se utilizan principalmente los métodos de Schwarz, en los que los subdominios se superponen entre sí. Esto proporciona resultados precisos, pero no es conveniente si las intersecciones de las regiones son demasiado complejas. Por tanto, un matemático de RUDN University junto con colegas de Hungría y Francia propusieron un nuevo algoritmo que facilita la descomposición. Los subdominios no se superponen, el resultado es preciso y el tiempo de los cálculos es mucho menor.

"Hasta ahora, la mayoría de las investigaciones sobre el método de descomposición de mencionada área de estudio se han basado en los métodos de Schwarz. El primer y único intento de tratar con la descomposición sin superposición concluyó que las iteraciones ocurren simultáneamente en los subdominios y en los límites entre ellos. Y para esto, se debe determinar el esquema numérico de cálculos para toda el área global", dijo Guillaume Gbikpi-Benissan, empleado de la Academia de Ingeniería, RUDN University.

El matemático junto con su equipo han propuesto un algoritmo basado en el método Gauss-Seidel. La esencia de esto radica en que el algoritmo de cálculo no comienza simultáneamente en toda el área, sino alternativamente en los subdominios y límites entre ellos. Como resultado se logra que los valores obtenidos durante cada iteración dentro del subdominio se pueden usar inmediatamente para los cálculos en el límite sin operaciones adicionales.

El nuevo algoritmo se probó con la ecuación de Poisson y la ecuación de momentum de Cauchy. La primera se usa, por ejemplo, para describir el campo electrostático, la segunda, en hidrodinámica, para describir el movimiento de los fluidos. Para ambas ecuaciones, el nuevo método resultó ser más rápido que el estándar. Este algoritmo permite ahorrar hasta un 50% de tiempo. Cuando el área se divide en 720 subdominios, el nuevo algoritmo resuelve la ecuación de Poisson en 84 segundos, mientras que el clásico lo realiza en 170 segundos. Además, el número de iteraciones necesarias disminuye mientras aumenta el número de subdominios.

"Este es un comportamiento bastante interesante y puede explicarse de la siguiente manera: la frecuencia de alternancia de los cálculos en los subdominios y en los límites aumenta a medida que el tamaño de los subdominios disminuye y aparecen más límites. Nuestros resultados crean nuevas oportunidades y dan paso a investigaciones prometedoras sobre el paradigma de la computación asincrónica", comentó Guillaume Gbikpi-Benissan, empleado de la Academia de Ingeniería, RUDN University.