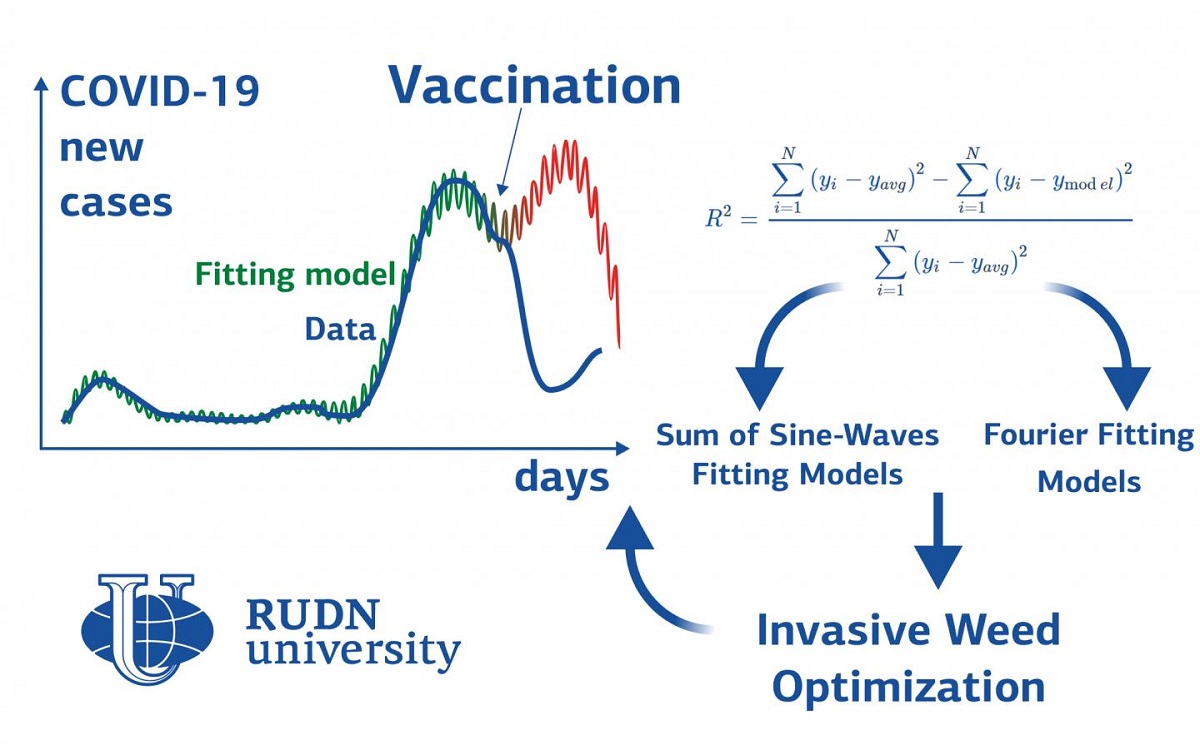
Matemática de RUDN University construyó un modelo de propagación de la COVID-19 que muestra cómo la vacunación afecta el curso de la pandemia
La tasa de propagación de una epidemia dentro de un país depende, entre otras cosas, de las condiciones climáticas del mismo: temperatura, humedad y vientos. Por ejemplo, en la estación fría, el aire seco seca la mucosa nasal (primera barrera contra el virus) y, por lo tanto, una persona se infecta más rápido. Las altas temperaturas, por otro lado, evitan que el virus se multiplique. Basándose en estas consideraciones, la profesora de RUDN University María Alessandra Ragusa, junto con colegas de Egipto e Italia, construyó modelos de propagación de la COVID-19 por separado para tres grupos de países con diferentes condiciones climáticas. Resultó que el modelo predice con precisión el curso posterior de la epidemia, pero solo hasta que el efecto de la vacunación comienza a manifestarse.
«El principal problema en el estudio de epidemias es cómo predecir el comportamiento de la enfermedad, cuántas personas se infectarán en el futuro, determinar el pico de la pandemia, la duración de la segunda ola de la enfermedad y el número total de muertes una vez concluida la pandemia. Usamos modelos de regresión modernos para modelar nuevos casos de la enfermedad en diferentes países y predecir las próximas oleadas de coronavirus», expresó María Alessandra Ragusa, catedrática de RUDN University.
Los matemáticos identificaron tres grupos de países. La primera categoría incluye países en los que la primera ola de la pandemia duró unos 180 días. Estos son los países con la tasa de propagación más baja, con una temperatura anual promedio de 15-38 ? (por ejemplo, Arabia Saudita, Egipto). En el segundo grupo de países (por ejemplo, Gran Bretaña, Alemania, Italia) con una temperatura anual promedio de 2-31 ?, la primera ola duró 90 días. Los países de este grupo se caracterizan por una tasa de infección media y «períodos de interrupción» cuando la tasa de propagación disminuye. El tercer grupo incluye países con la tasa de infección más alta y sin períodos de interrupción, con una temperatura anual promedio de 2-18 ?, por ejemplo, Estados Unidos y Rusia.
Para modelar, los matemáticos utilizaron datos de la OMS sobre el número de casos del 1 de marzo al 15 de noviembre de 2020. Los matemáticos de RUDN University han elegido los modelos de regresión más adecuados, es decir, métodos de estudio estadístico del efecto de varias variables sobre una sola magnitud. Las series de Fourier y la suma de senos fueron las más precisas para modelar casos de COVID-19. Esto significa que la curva de nuevos casos de la enfermedad se presenta como una suma de funciones de Fourier (se pueden representar como oscilaciones de cierta frecuencia y amplitud) o como una suma de senos ordinarios.
Como resultado, los matemáticos obtuvieron los valores calculados del pico de la segunda o tercera ola en los países estudiados. Diferentes modelos dieron aproximadamente los mismos pronósticos con una diferencia de varios días. Las predicciones obtenidas por los matemáticos se compararon con los datos disponibles en ese momento. Resultó que el modelo ofrece predicciones bastante precisas si el país no ha adoptado la vacunación masiva. Por ejemplo, el valor calculado del pico de casos nuevos en Egipto es 1481 al 11 de enero de 2021; en realidad, el pico se produjo el 31 de diciembre y se registraron 1418 casos. En el resto de los países, el modelo proporciona predicciones precisas hasta principios de 2021. Después de eso, el efecto de la vacunación comienza a influir y los valores calculados difieren de la realidad. Por ejemplo, para Alemania, los valores pronosticados y reales coinciden hasta aproximadamente el 15 de enero de 2021, y ya el 15 de febrero difieren aproximadamente 2,5 veces.
«En el futuro, planeamos desarrollar modelos predictivos, teniendo en cuenta cómo la vacunación afecta la tasa de propagación del virus», concluyó María Alessandra Ragusa, catedrática de RUDN University.
Los resultados han sido publicados en la revista Mathematics
Agrotecnólogo de la Universidad RUDN ha identificado genotipos de trigo que son resistentes a un patógeno fúngico peligroso que infecta las plantas incluso antes de que la nieve se derrita y reduzca los rendimientos.
Los ingenieros de la RUDN han calculado los parámetros de un sistema que puede evitar que las centrales eléctricas lunares se sobrecalienten. Estos desarrollos serán necesarios al planificar misiones lunares a largo plazo y colonizar el satélite.
Un matemático de la Universidad RUDN llamó redes neuronales que pueden ayudar a los médicos a interpretar los resultados del EEG y otros análisis de la actividad cerebral. El mejor de ellos funciona con una precisión de casi el 100%, mientras que no solo da el resultado, sino que explica por qué resultó de la manera que lo hizo.